sigh -- so many good books!

I was using my copy of Barlow's Tables (1952) to find square roots in graphing circles, and happened to notice an advertisement on the back cover for Engineers' Illustrated Thesaurus 1952, which looks like an awesome book! It has 'over 8,000 illustrations of mechanical movements, machine parts and details...' just the few graphics in the advertisement are intriguing -- but since we went to an auction (for household things) today, books will have to wait a bit longer.

I have a new chapter for the math problem -- but I have to take the time to work out a new diagram and decide if I am going to work on this part separate from the original, or as a continuation of the original problem. I think separately, at the moment.

Some stuff on gears

The math problem is a piece towards investigating gears, but also, in the other direction, towards the geometry and trigonometry behind the shapes and motions happening in the gears -- towards some grasp of calculus... did I lose you yet? I'm still figuring out how many pieces, and where from, I need to satisfy my curiosity.

Type of Gears <--some cool lego stuff here too
Epicyclic gear trains and the math calculations of
this page on timing gears from this online book Construction Mechanic Basic V.1

this is a cool site -- not quite what I am working on now, but soon... clockworks

Bisecting secants in an circumcircular curve

I'm bashing a bit on this problem that has to do with an element of epicycloidal curves. However, this particular element is really about secants.

The Problem:
This is the rough diagram I drew of the problem, as far as I have gotten:
Relevant corrections (but no solutions) will be appreciated

Pathway to the solution:
The following math was contributed by a friend, Dasunt, to solve the red and pink lines.

Radius of Circle = AZ = CZ = BZ
by definition: AC = BC
known side: AB
AD = BD = (1/2 AB)
sqrt( AZ² - AD² ) = DZ
CZ - DZ = CD
sqrt( AD² + CD² ) = AC = (by definition) CB
Sides AC and BC are now known.

I made the graphics here from base drawings found online - if you want me to I will remove them and put up POV-Rayed examples when I get a spare moment. MLWM 2006

Found Links that I want to remember:

---

I found this post about science blogging on Science & Politics blog (hopped to from Confessions of a Science Librarian which had a great set of links!)

Oh I'm Happy! (I found my books!)

We are still unpacking from our move to Tennessee last April, and there are books I have yet to locate! (we have a LARGE collection)

This morning I found my much-missed 1936 Sisam & Atchison copy of Analytic Geometry (I had misidentified it before) I am happy!

I still haven't found The Way we Think, but did also locate 'The Elegant Universe'.. which so far I hadn't noticed was missing...

Also found: The 1895 set of 'Stories by English Authors' that I was truly hoping was safe (I promised the lady who sold them to me ten years ago that I would take care of them!) I only own 7 of the 9 -- missing 'Ireland' and 'The Sea.' All but 'Germany' (of mine) are in excellent condition.

UPDATE: The Way We Think is found! -- but I'm in a math kick now...

on Leonardo da Vinci (again)

I spoke some in another post about Leonardo da Vinci -- and today have found more that is on the same cue.

Leonardo da Vinci said:

"Let no one read me who is not a mathematician."

I guess I really do need to study more ;o)

from the book 'The Age of Adventure' 1956 - compiled by Giorgio De Santillana

It begins with a chapter again telling how Leonardo did not lay out his theories as did other learned men and 'philosophers' of the age -- but goes on to say this...

The universe that Leonardo saw was a logically tight universe, fit for profound meditation; but he was not interested in trying for what he felt could not be done, namely, translating the universe into purely verbal tightness.

He refused to think in words only, as the scholastics did. He was searching for a passage towards a new language. What that language itself was, Leonardo tried to establish through soundings that range over many depths, from the portrayal of form to applied mathematics.

Dartmouth's outline of Leonardo speaks a bit more about Leonardo's mathematics and just above that, his trouble with the NeoPlatonists, the philosophers mentioned above.

The paths I myself am looking to take are very well-trodden. Studying mathematics is not going to tell me everything I want to know. However, a deep scanning of many related subjects (which will require knowing math to do) will bring me closer. Leonardo da Vinci's life's work is exemplary of this.

In which I get into some cognitive philosophy -- you may want to look away

For a really long time, I've been interested in the way we think. It is one of the most brain somersaulting things a human being can focus on, the process with which they process information... imho


I don't have a whole lot of time for myself lately -- but I've been trying to be productive with my thought processes.

While driving back from the post office (tax time), I made this little postulate about it.

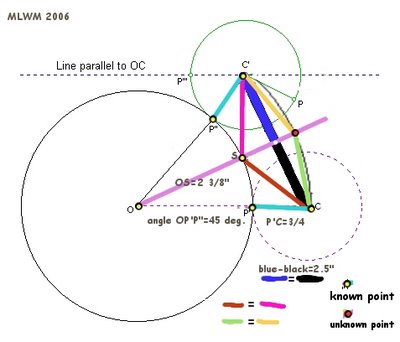
click to enlarge and read text

writing/speaking <--> conscious flow <--> philosophy/study of logic <--> experiment/diagram/actual logic/mathematics <--> drawing/sculpting/building <-->images/symbols/pattern recogition/making connections <--> subconscious flow

yes I'm getting into muddy waters here, but maybe I need to study the mud and the water atm to find the truth.


It seems like there is a point in that continuum (which is not absolute, and is my own mock-up) that is almost like an 'access point.' At some stage there, my brain stops working in symbols and images, and begins to make logic and words. Logic and words are the key to expressing oneself in the physical world (although drawings and sculptures could, they are not understood as absolutely, especially by the masses).

I need to exercise that region of my thought process until I can either expand or improve that access point. Maybe math is the way to do this -- or it will lead the way to it. Maybe a bit of A, B, and C are required.. art, math and philosophy(study), in order to attain this goal.

I'm sounding flaky even to myself here, but somewhere here is a kernel of truth that will help, somehow, to a better and greater understanding of what I really want to know. Know theyself, in order to know the world?

The results may yield the formula, as much as the formula yields the results. But what truly yields the truth, is something that the formula and the results hold in common.. the process -- the calculation, the transfiguration.

Book Links:

---

The Way We Think: Conceptual Blending and the Mind's Hidden Complexities book.. although I've read part of it and need to read some more.. especially after this.

I might have to look into getting this one afterwards.. if I can think straight after all of this ;o) Mappings in Thought and Language --"This book examines a central component of meaning construction; the mappings that link mental spaces. A deep result of the research is the fact that the same principles operate at the highest levels of scientific, artistic, and literary thought as do the lower levels of elementary understanding and sentence meaning. Some key cognitive operations are analogical mappings, conceptual integration and blending, discourse management, induction, and recursion..." from card catalog desc at Amazon.

Online articles and archives

---

Cognitive questions archive

Cool Blogs

---

Mixing Memory <--look at all the past archives!

Goedel, Hofsteader and LeibnizG.H.L within G.E.B?

I was reading a selection from Leibniz' 'Dialogue on the Connection Between Things and Words' (1677) today and was getting 'deja vu' from Douglas Hofsteader's Goedel, Escher Bach (GEB).

I went out looking and here is why: On Goedel's Philosophy of Mathematics, specifically his part on the existence of mathematical objects. So of course, if Goedel refers to Leibniz (which apparently he does), and Hofsteader refers to Godel, on something much the same subject as Leibniz.. it comes around logically that one will sound very much like the other -- even though it comes about it thirdhand(?).

Anyway -- what I am babbling on about is this:

I only mean that characters must show, when they are used in demonstrations, some kind of connection, grouping and order which are also found in the objects, and that this is required, if not in the single words -- though it were better so -- then at least in their union and connection.

This order and correspondence at least must be present in all languages, though in different ways. And that leaves me with hope ...For even though characters are as such arbitrary, there is still in their application and connection something valid which is not arbitrary; namely, a relationship which exists between them and things, and consequently, definite relations among all the different characters used to express the same things.

And this relationship, this connection is the foundation of truth. For this explains why no matter which characters we use, the result remains the same (as in algebra), or at least, the rsults which we find are equivalent and correspond to one another in definite ways. Some kind of characters is surely always required in thinking.

quot3ed from Leibniz' Dialogue on the Connections Between Things and Words - 1677

If you've read G.E.B -- you will find a ring of familiarity in the talk about 'arbitrary symbols' and the things they represent. I'll have to go back through that book myself and see if (probably), how and where he himself references Leibniz... it has been several years and G.E.B is one LONG and heavy-reading book.

Leonardo da Vinci - beyond the artist

Wikipedia's article on Leondardo da Vinci

Free e books at Project Gutenberg:
Leonardo's Notebooks (text only)

Online Sites:
Leonardo's Machines <--nice site
A good many Leonardo da Vinci illustrations at this site, including medical illustrations (anatomical drawings).

I found this interesting, about where Leonardo got his books and what was in them-->Leondardo Da Vinci and Ancient Printed Medical Tests HTML version of a PDF

Of course Da Vinci was an artist..
but he was also ( schooled in / skilled at ) mechanics, anatomy, geometry and a wide range of subjects. I read his notebooks my first year at college -- not ALL of it, mind you.. there is so much there to absorb -- but just seeing the wide range of subjects and taking some of it in, is enough to spark anyone into some sort of creative thought ;o)

Odd though.. my sketchbooks did start to look more and more like that afterwards! They still do.

I read in my book 'The History of Mathematics' that most of the math Leonardo did in his notebooks, was incomplete. He would get to a point where he couldn't figure out the calculations, and just trail off... He would get frustrated. I identify with that. Then he would go build a model, or work on something else for a while. He was a genius, true, but even geniuses must get stumped once in a while, on something. He never lost his curiosity though - and that is important. He always wanted to know, or at least to seek, even if he found he could not always understand.

Back to sketching...

Planetary and Epicyclic Gears (and notes)

We got some sleep last night - but also watched some Netflix-generated MacGyver... it is nostalgic to see him pull down a helicopter with a car-winch (season 1 - ep 1) and etc etc.. things you don't really notice when you are a kid, that wouldn't really work! I also liked the chocolate bars plugging up a large acid leak in the pilot... would have to do some research on that one... force behind it, size of the bars, bare hands etc etc...

Here is where my brain was this morning (spec. planetary gear systems and pulleys) about 8 am. I had drawn a little mechanical doodle while in a morning meeting. Actually, I had to ask a few people if they recognized it! I couldn't remember what it was exactly... just that I had seen it before and it made sense. It was something close to the epicyclic gear in the second article.

The worst thing I've noticed as I get older, is that the longer I don't use some bit of knowledge, the easier it is for me to forget the specifics of it.. and get confused by the generalities as well.

Online Reference Links

---

Planetary Gears: Online article : How stuff works
Epicyclic Gears : Online article : Sun and Planet Epicyclic Train
Online Article: This one has a nice 3D image in it
Online Chapter: A good reference on Gears in general with lots of good equations and diagrams.

Oh wow!
I can buy a science toy to try it out *wishlist* --> Planetary Gear Box Set

I have a nice little set of pulleys, magnets, pipe-fittings, faucet valves and other physics toys that are at home. It has been a while since I played around with them. :o(

Back to Python Land! I have some web forms to generate and process dynamically. I worked on them some yesterday, but the plan changed at the meeting.. *sigh* so I have to go back and rework them to the new specs.

Oh my can I get distracted -->
I'm linking these so I can read them later and do work now

---

Propositionnal Calculus
Logical Connectives

Science News articles

and now a few short glimpses at what is going out there in the world, before I put my nose back into these books.

Found at EurkeAlert!

---

Gases in One Dimension -- Not Your Typical Desk Toy <--great! Chaos theory, how it does attract the imagination...

'Tensegrity' structures -- structures that deform on will... odd but interesting concepts! How would you like to drive over a bridge or go into a building that can fold up like a wallet or adjust its shape to the weather or earth movements? Really great topic.

Venus Express space probe arrives in orbit. Will we get just pictures, or relevant scientific answers?

new steps towards Organic Light-Emitting Devices? wow. to replace flourescent lights? no more flicker to drive me crazy? ;o)

Here is a quiz How Geeky Are You? from Newsweek. I got a 50% -- really, just because you don't use your cell phone to take pictures (I have a rocking digital camera for that.. so sue me!) or play Warcraft, text-message people to boredom, or rely on TiVo to get your entertainment.... doesn't mean you aren't a serious geek. Where are the real questions about what you DO do, or what you know? Anyway.. that is my rant. Newsweek needs to get out of pop culture 'geekery' and back to brain food.

Free Books on Geometry at Project Gutenberg

There are three (so far) books at Project Gutenberg that are free and available to the public for download.
Please help support Project Gutenberg!
If you have a book that qualifies.. you can volunteer to transcribe it, or proofread another person's transcription!

The Foundations of Geometry by David Hilbert
Non-Euclidean Geometry by Henry Manning
An Elementary Course in Synthetic Projective Geometry by Norman Lehmer

In addtion, there is the following which has a chapter on Analytic Geometry (ch 15):
History of Modern Mathematics by David Eugene Smith

Quoting Leibniz, on types of geometry

a little Leibniz and I do mean 'a little'... I found this an interesting and nicely put way of examining the early geometers.. and linking them for later research.

Quote:

---

Since theorems serve only to abbreviate or guide the solution of problems and since all theory should assist practise, all we need to do in order to judge the variety of kinds of geometry is to consider its problems.

The problems of geometery are about straight lines or curves, and presuppose only the magnitude of some lines or figures, straight or curved. To the latter sort belong the problems of finding centers of gravity, and consequently, a good many problems of mechanics.

Thus we may say that there are two kinds of geometry, an Apollonian and an Archimedian; the first was revived by Viète and Descartes, the second by Galileo and Cavalieri.

From a 1951 version of 'Leibniz' selections, Ch 1, pg 5. : cited there from 'General Geometry and the Method of Universals, (1674)

some neat links:
six species of information architect

oh what a cool blog! --> Space from the inside, and outside at A Kind of Bastard Reasoning. Just read the top header and you'll know why I am reeling with curiosity and awe that this exists in the blogosphere!

Optic(k)s

I want this book too:
Opticks: Or a Treatise of the Reflections, Refractions, Inflections & Colours of Light-Based on the Fourth Edition London, 1730
by Sir Isaac Newton

The ideas of lenses, telescopes and microscopes are bouncing in my head along with the various problems of geometry I have been researching. It is coming through in my artwork as diagrams of the human eye, angles of reflection and dilation of images.

I've also found it just plain fun to play around on bristol with my compass and a black ink pen ;o) These little sketches are becoming reminiscent of Wassily Kandinsky or Paul Klee.

Understanding and Plotting the Curve

The next part of my research is about understanding the curved line better, so as to better represent it in artworks and use the ideas behind it to make statements about real space.

Online Article: Asymptotes

On the geek desk: geometry, optics and related books

I'm sure the urge for 20-something American women to do math doesn't happen out-of-the-blue much, at least not around here, in this day and age... but I had gotten a few questions in my head this week that wouldn't let my curiosity give up, until they were answered.

The Questions (that started it all)

---

When parallel lines of light hit a certain type of lens -- what does it look like : Answered, easy when I looked for it. It was a convergent type of lens -- and they all DUH converge... onto one point, then go back out from there...

Review the basic properties of circles, curves and angles via some good OLD geometry resources. For some reason, the language used in the older books just hits the spot for me -- it clicks where newer books usually leave me staring at the page blankly.

Right now, I'm drinking strong coffee, and working out connections between geometry, art and optics in a tablet with nice black ink. It is really inspiring some creative art as well. Better pictures of the real art later ;o)

My Books (on the Geek Desk)

---

Leibniz Selections: c. 1951 Charles Scribner's Sons
Elementary Plane Geometry Self-Taught: Lawrence A. Barrett Little Blue Book No. 748 marked 3/16/1929 by original owner
Practical Physics: by N. Henry Black and Harvey N. Davis 1923 The MacMillan Company
Algebra and Trigonometry: Rees, Spark and Rees 1975
University Physics, Jeff Sanny & William Moebs 1996 (vol.2 Optics)
Copied from book at library (reference book) : the Geometry (book 1) by Rene Descartes

On the Geek Screen

---

Online Article: René Descartes' Curve-Drawing Devices: Experiments in the Relations Between Mechanical Motion and Symbolic Language
Online Article: Convergent lens and the real image

Online Figures: Deviation of rays by convergent lens

Online PDF (excellent!) : Geometric Optics <--dream come true resource.

Amazon wishlist

---

Euclid's Geometry
Archimedes
Euclid's window looks interesting
Descartes' Geometry (full version)

For my own memory: Essentials of Analytic Geometry 1939 by Professor Raymond Brinks of the University of Minnesota. I have a copy of this somewhere!! I haven't been able to find it since our move :o( It was the first book that made polar coordinates click in my head.